Recursive Tail Calls and Trampolines in Swift
Posted on May 5, 2016 中文版
Update 10/17:This post has been verified with Swift 4, no changes required.
Update 10/16:This post has been updated to Swift 3.
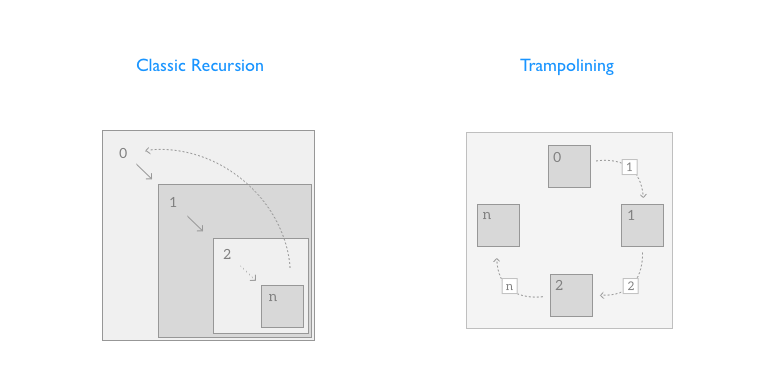
The use of recursion can often lead to a cleaner implementation of your algorithms but when compared with implementations based on loops, recursive ones incur in the additional cost of allocating and managing a new stack frame for every method call performed, something that makes the recursive implementation slower and that can also quickly lead to stack exhaustion (aka stack overflow).
To avoid the risk of overflowing the stack, the recommended approach suggests to rewrite your algorithm employing tail recursion to leverage the tail call optimization that some compilers provide.
But what’s the difference between recursion and tail recursion and what are those compilers actually doing to solve the issues above?
Tail recursion differs from generic recursion for the fact that the result of the recursive call is always returned without any additional manipulation to the caller and calculation are performed through an accumulator variable that passes partial results to the successive recursive calls along the chain, until the end of the recursion is reached.
If this definition seems confusing, an example in the next section will make it more clear, for now you just need to know that this specific kind of recursion can be optimized and these recursive algorithms can be easily identified and converted by a compiler to a more efficient loop-based implementation, not affected by stack size limitations.
But in Swift, we can’t rely on the fact that the compiler will always perform the tail call elimination described above in every circumstance.
This limitation has already been discussed on Natasha’s blog before and some work has been done on the draft of a proposal that aimed at adding a few new attributes that would have made the behavior of the optimizer more verifiable, allowing to explicitly state which recursive method call we expected to be optimized (and if that didn’t happen an error would have been thrown).
In this post we’ll see how the lack of predictable tail call elimination in Swift could be overcome using trampolines and a few alternatives to recursion will be described.
Get the playground for this post from GitHub or zipped.
Triangular numbers with recursion
Let’s see an example of an algorithm that calculates the n-th triangular number recursively:
func tri(n:Int)->Int{
if n <= 0 {
return 0
}
return n+tri(n: n-1)
}
tri(n: 300) //45150
In this example of simple recursion, the result of the recursive call is added to the value passed as parameter and the result of our initial method call tri(300) will be the sum of all those integer values, chained together with recursion.
To improve this algorithm adding tail recursion, we’ll add an accumulator that will be passed along to the next call:
func ttri(n:Int, acc:Int=0)->Int {
if n<1 {
return acc
}
return ttri(n: n-1,acc:acc+n)
}
ttri(n: 300) //45150
Notice how the result of this algorithm is now built with the accumulator and the last step of the recursion just returns the accumulator value to complete the calculation.
But both functions will crash your application or playground when invoked with a big enough integer as parameter. Let’s see how trampolines can solve this issue.
Trampolines
The idea behind trampolines is actually quite simple.
A trampoline is not much more than a loop that executes iteratively functions that can either return the next function in the sequence (in form of a thunk or continuation, a data structure that contains the information needed to perform a specific function call) or another kind of value (in this case the content of the accumulator) to signal the end of the iteration.
The tail recursive function we wrote will have to be slightly modified if we want to execute it sequentially through a trampoline, we’ll need to rewrite it in continuation-passing style.
Update
As @oisdk pointed out, the modified function we’ll see below will only slightly resemble actual CPS:
Here, closures are letting you simulate lazy evaluation to do pseudo tail-call optimisation. In Continuation-Passing style, you pass in a continuation as an extra parameter to your recursive function. The continuation represents what happens after the function it’s being passed into is called. Then, to evaluate the continuation, you (usually) pass in the identity function. This lets you transform non tail-recursive functions into tail-recursive ones. Obviously, since TCO isn’t guaranteed in Swift, this isn’t very useful.
Regardless, here’s what the triangular numbers example would look like in CPS:
func triCont(n: Int, cont:@escaping Int -> Int) -> Int { return n <= 1 ? cont(1) : triCont(n: n-1) { r in cont(r+n) } } func id<A>(x: A) -> A { return x } triCont(n: 10, cont: id) // 55Thanks for the great explanation.
Instead of performing directly a recursive call, our ttri function will now return an object that will wrap the actual call we performed previously and once the point where the execution should complete will be reached, we’ll return a sentinel value with the content on the accumulator.
We start defining a Result enum that represents the range of values that the modified recursive function will be able to return: a .Done value that will signal the end of the recursion and that will contain the accumulator, and a .Call value that will contain a closure with the next function call to perform.
enum Result<A>{
case Done(A)
case Call(()->Result<A>)
}
And after that we define a new function, containing the modified ttri tail recursive function and a section of code implementing the trampoline. This last part is usually contained in a separate function, but in this example everything will be kept together to make the code more readable.
func tritr(n:Int)->Int {
func ttri(n:Int, acc:Int=0)->Result<Int> {
if n<1 {
return .Done(acc)
}
return .Call({
()->Result<Int> in
return ttri(n: n-1,acc: acc+n)
})
}
// Trampoline section
let acc = 0
var res = ttri(n: n,acc:acc)
while true {
switch res {
case let .Done(accu):
return accu
case let .Call(f):
res = f()
}
}
}
tritr(300)
Once you wrap your head around it, understanding what is happening in the trampoline section it’s not too hard.
After an initial call to the ttri method to bootstrap the trampoline, the functions contained in the .Call enums are executed in sequence while the value of the accumulator is being updated at each step:
return .Call({
()->Result<Int> in
return ttri(n: n-1,acc: acc+n)
})
Even if the code is different, the behavior it’s still the same of our original recursive call.
Once we are done, the ttri function returns a .Done enum with the final result to be returned.
And even if this implementation is slower than the original one for all the code needed to operate the trampoline that was added, this version solves our biggest issue related to stack exhaustion, we’ll now be able to calculate every triangular number our heart desires… until we hit the size limit for integers.
Update: Following a suggestion from @oisdk, the design of the ttri function could be improved using the often forgotten @autoclosure attribute:
func call<A>(c:@escaping () -> Result<A>) -> Result<A> {
return .Call(c)
}
func ttri(n: Int, acc:Int=1) -> Result<Int> {
return n <= 1 ? .Done(acc) : call(c: tri(n: n-1, acc: acc+n))
}
Before we move on, let me add one more thing about that example, enclosing a block of code within a while true it’s usually a code smell but this time I did it to make the example more compact, a more proper loop check would have looked something like this:
while case .Call(_) = res {
switch res {
case let .Done(accu):
return accu
case let .Call(f):
res = f()
}
}
if case let .Done(ac) = res {
return ac
}
return -1
And for an even more proper check, since we are using enums with associated values, we should have implemented the comparison operator for this specific enum and check for not done on top of the loop.
Now that the basics of how trampolines work are explained, we can build a generic function that given a function converted to use the Result enum, returns a closure that will execute the original function with a trampoline, hiding what’s happening under the hood:
func withTrampoline<V,A>(f:@escaping (V,A)->Result<A>) -> ((V,A)->A){
return { (value:V,accumulator:A)->A in
var res = f(value,accumulator)
while true {
switch res {
case let .Done(accu):
return accu
case let .Call(f):
res = f()
}
}
}
}
The body of the closure we return is essentially what we had in the trampoline section in the previous example and withTrampoline expects as parameter a function with the form (V,A)->Result<A>, that is what we had before.
The more obvious difference with the previous version is that since we can’t initialize the generic accumulator A because we don’t know yet its concrete type, we’ll need to expose it as a parameter in the returned function, a minor annoyance.
Let’s see how to use our new utility function:
var fin: (_ n:Int, _ a:Int) -> Result<Int> = {_,_ in .Done(0)}
fin = { (n:Int, a:Int) -> Result<Int> in
if n<1 {
return .Done(a)
}
return .Call({
()->Result<Int> in
return fin(n-1,a+n)
})
}
let f = withTrampoline(fin)
f(30,0)
This is probably a bit more verbose than what you expected.
Since we need a reference to the current function inside the closure to use it in the thunk, we must declare a dummy reference before declaring the actual closure and use that valid reference in our function.
Declaring the fin closure directly without the dummy and attempting to use it would get us a Variable used within its own initial value error. If you feel adventurous, an alternative to this ugly workaround consists in using a Z Combinator.
But if moving away from the traditional trampoline design is not an issue, we can improve what we have above simplifying the Result enum and keeping track of the function to call inside the trampoline instead of saving it as an associated value of the enum:
enum Result2<V,A>{
case Done(A)
case Call(V, A)
}
func withTrampoline2<V,A>(f:@escaping (V,A)->Result2<V,A>) -> ((V,A)->A){
return { (value:V,accumulator:A)->A in
var res = f(value,accumulator)
while true {
switch res {
case let .Done(accu):
return accu
case let .Call(num, accu):
res = f(num,accu)
}
}
}
}
let f2 = withTrampoline2 { (n:Int, a:Int) -> Result2<Int, Int> in
if n<1 {
return .Done(a)
}
return .Call(n-1,a+n)
}
f2(30,0)
Way cleaner and compact.
Get the playground for this post from GitHub or zipped.
Swifty Alternatives to recursion
As you already know if you’ve read some of the posts in the Swift and the functional approach series, Swift provides a few features that can be helpful to build alternative implementations for algorithms that are usually implemented recursively.
For example, triangular numbers could have been calculated with just a simple functional one liner using reduce:
(1...30).reduce(0,+) //465
Or we could have created a Sequence or an Iterator to generate a sequence with all the possible triangular numbers:
class TriangularSequence :Sequence {
func makeIterator() -> AnyIterator<Int> {
var i = 0
var acc = 0
return AnyIterator(body:{
print("# Returning "+String(i))
i=i+1
acc = acc + i
return acc
})
}
}
var fs = TriangularSequence().makeIterator()
for i in 1...30 {
print(fs.next())
}
And these are only two alternative implementations we could have built using what Swift provides.
Closing Thoughts
This post describes the limitations that Swift has in regard to recursion and shows how trampolines, the by-the-book workaround for languages lacking TCO, could be implemented in Swift. But, am i advocating the use of trampolines in your code?
Definitely not.
In Swift, considering that the language is not purely functional, what could be solved with a complex construct like trampolines can always be solved in a better way (producing code that is more readable and with a behavior easier to grasp) using one of the features the language provide, don’t over-engineer your code, your future self will be glad you didn’t.
Thanks to @oisdk for his insightful comments.
Did you like this article? Let me know on Twitter!